
8/12 Går det att skriva talen 1 till 100 i en rad så att skillnaden mellan två intilliggande tal alltid är 50 eller mer?
9/12 I en adventsljusstake med fyra likadana ljus har man, som man brukar göra, tänt det första ljuset den första veckan, nästa vecka det första och andra osv. Varje dag hade man ljusstaken tänd 15 min. En dag var det första och tredje ljuset tillsammans lika långa som det fjärde, som ännu inte tänts. Hur mycket var det då kvar av det andra ljuset?
10/12 Vilka figurer kan dölja sig bakom korten? Vilka är möjliga? Vilka är inte möjliga?

11/12 På en vanlig tärning finns ettan alltid mittemot sexan, tvåan mittemot femman och trean mittemot fyran. Hanna slår en röd och en grön tärning. Hon multiplicerar antalet prickar på tärningarna och skriver upp resultatet. Sedan vänder hon den röda tärningen upp och ner, multiplicerar åter antalet prickar och antecknar resultatet. Hon gör samma sak efter att ha vänt den gröna tärningen och slutligen en fjärde gång efter att ha vänt den röda tärningen tillbaka. Därefter adderar hon produkterna. Vilken är den största summan, hon kan få på detta sätt?
12/12 Finns det två tresiffriga tal vars summa är fyrsiffrig och där alla siffrorna i dessa tre tal är olika?
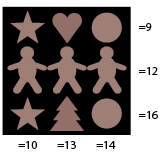
13/12 Tomtefar bakar pepparkakor till julmarknaden. Han funderar över priset på kakorna och summerar för varje rad och kolumn. Men vad kostar gubben, stjärnan, hjärtat, granen och cirkeln var och en för sig?
14/12Kan kanterna på en kub numreras med talen 1 till 12 så att summan av de fyra talen vid kanterna vid en sida blir densamma för alla kubens sidor?
Inga kommentarer:
Skicka en kommentar